An Illustrated Guide to Covariance and Contravariance in Kotlin

Generics can often seem confusing. How often have you started to solve a problem with generics, only to realize that they don’t quite work like you thought they did?

The good news is that there are some simple, foundational concepts that underpin generic variance. And once you understand those concepts, you won’t have to memorize acronyms or resort to trial-and-error - you’ll simply understand how and why they work!

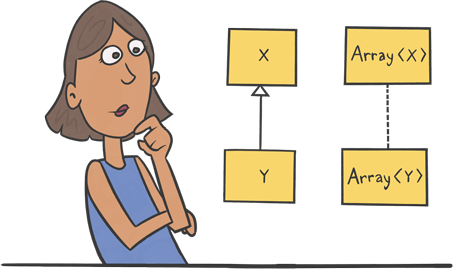
In this article, I’m going to cover these foundational concepts, and then demonstrate how they play out in Kotlin class and interface inheritance. Then in the next article, I’ll uncover how these same concepts play out for generics and type projections.

Ready? Let’s go!

It’s All About Subtypes

When it comes to generics, what trips us up the most? Subtyping.

Sure, we know intuitively that a Dog is a subtype of an Animal. But it’s easy to get confused about why an Array<Dog> isn’t a subtype of an Array<Animal>.

Instead of using intuition alone to understand subtypes, let’s identify some actual characteristics that a subtype must have, by definition.

In order for a subtype to truly be a subtype, you must be able to swap one in as a replacement for its supertype, and the rest of the code shouldn’t notice anything different. For example, in order for SubGizmo to be a subtype of Gizmo, nothing must break when code that expects a Gizmo actually interacts with a SubGizmo instead.

Now, when we say “shouldn’t notice anything different” and “nothing must break” - we could be talking about a lot of things. In this article, we’re going to focus on function calls, and the types involved in those calls.¹

Arguments and Results

As you know, there are two sides to a function:

1. The arguments that the calling code sends to the function.
2. The result that the function returns to the calling code.

Let’s visualize a good old-fashioned function call like this:

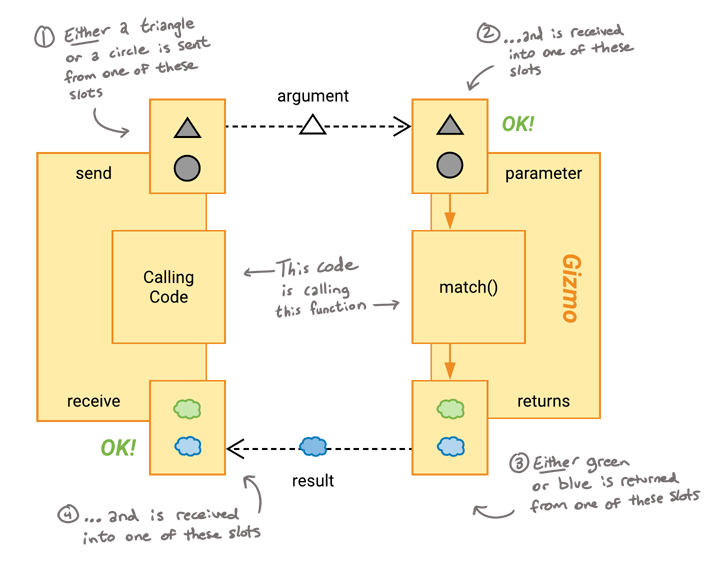
On the left, we have some code that wants to match a shape to a color. To do that, it interacts with a class on the right, called Gizmo, by invoking its match() function. Here’s what the calling code knows about Gizmo’s match() function:

1. It will accept a single argument of either a triangle or a circle, and…
2. It will respond with a color of either green or blue.

Now, this calling code has been using Gizmo successfully for a long, long time. But today, we’re going to secretly switch out Gizmo with our new SubGizmo (which, of course, is a subtype of Gizmo!).

Narrowing Arguments

This new subtype is designed to work specifically with the circle shape only, so it won’t support triangles. Let’s see how it goes:

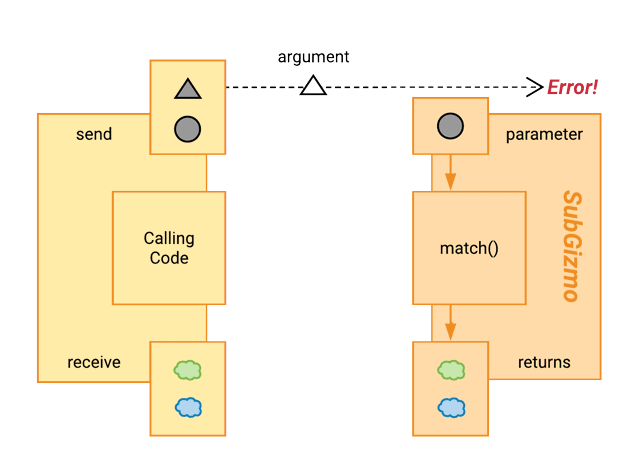
Aww… that didn’t go very well.

Our calling code has been used to sending triangles to the Gizmo, but this new subtype didn’t have a slot for it, so we ended up with an error. If we’re going to substitute a SubGizmo for a Gizmo, it looks like it’ll need to continue supporting the same kinds of arguments that Gizmo has always supported.

Expanding Returns

Let’s modify our SubGizmo again! Instead of changing the supported argument types, we’ll continue to support both triangle and circle. But, this time, we’ll update the return types – instead of just green or blue, it can also return red! Let’s fire things up and see how they do.

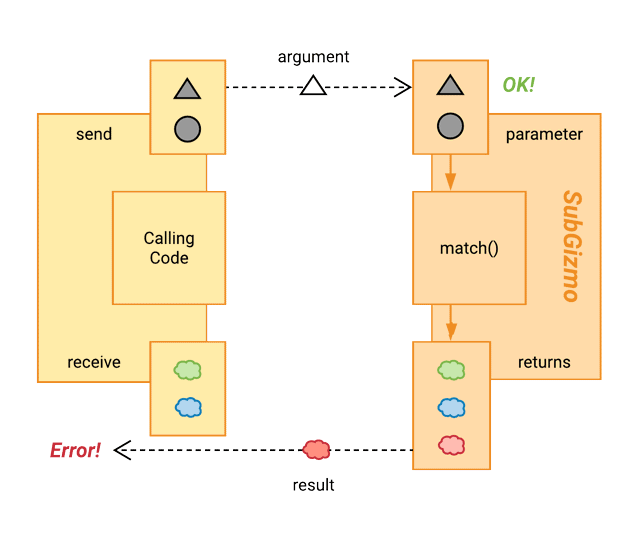
Blast! We’ve got another error.

Because the calling code only expects to receive green or blue, returning red didn’t work.

So we’ve discovered a few things. In order for SubGizmo to truly be a Gizmo, it must continue to accept the same kinds of arguments as Gizmo, and it must not return a result type that Gizmo wouldn’t return.

Let’s write these out as rules. To make them look more official, we’ll put them in a gray box:

1. A subtype must accept all argument types that its supertype does.
2. A subtype must NOT return a result type that its supertype wouldn’t return.

But, hang on!

Let’s take another shot at creating a SubGizmo, but this time, instead of narrowing the range of argument types that it accepts, let’s expand it.

Expanding Arguments

In addition to the triangle and circle that Gizmo accepts, SubGizmo will also accept a new shape - a square.

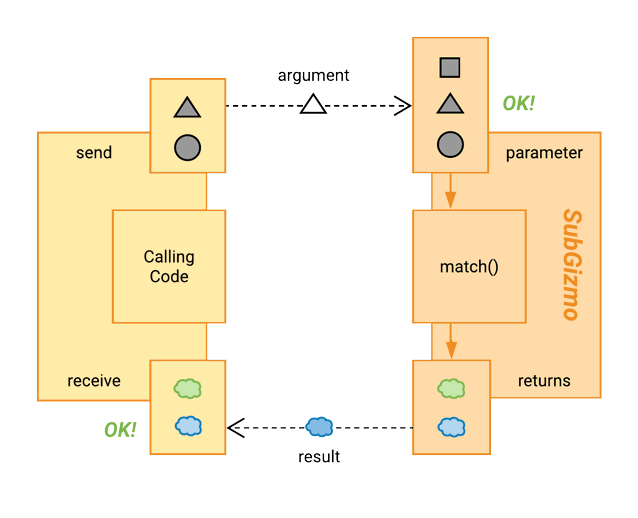
Now we’re getting somewhere!

Even though our calling code doesn’t know anything about the new square type that SubGizmo can accept, nothing will break, because triangle and circle are still supported. And those are the only kinds of shapes that this particular call site cares about. (Other code that interacts with SubGizmo might know that it can accept a square, of course, but we haven’t broken anything for code that uses it as just a Gizmo).

Let’s do one more thing.

Narrowing Returns

Instead of expanding the range of result types that it can return, let’s narrow it. Even though Gizmo can return either green or blue, our latest incarnation of SubGizmo will only ever return green:

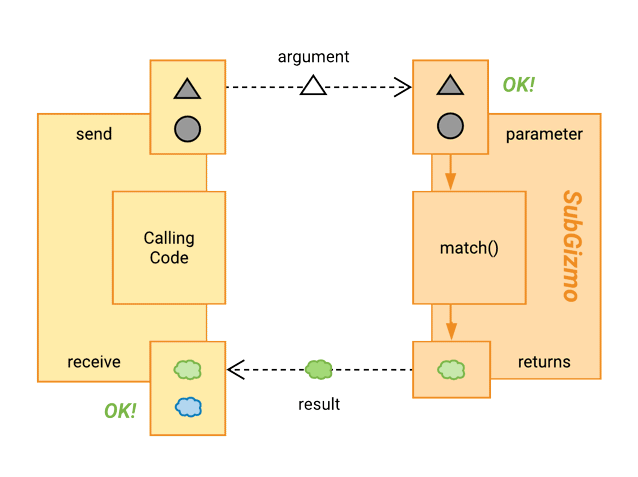
Success again!

The calling code can accept either color, and since SubGizmo only ever returns green, nothing will break.

Refining the Rules

So we can refine our rules from above, taking into account that it’s totally fine for the subtype to expand the range of argument types, and to narrow the range of response types:

1. A subtype must accept at least the same range of types as its supertype declares.
2. A subtype must return at most the same range of types as its supertype declares.

These two rules form the basis of variance. Once you’ve got these under your belt, you’ll be able to reason your way through just about anything related to variance.

Talking about shapes and colors has been nice for illustration, but let’s make this more concrete. Instead of matching shapes to colors, we’ll modify our Gizmo to match up compatible animals, so that they can make friends with each other and frolic together in the backyard.

Here’s a hierarchy of Animal types:

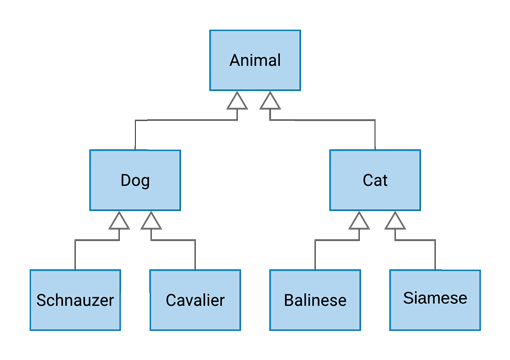
Let’s see how Gizmo and SubGizmo might work with this tree of types.

Accepting Arguments - Contravariance

Rule #1 above stated:

A subtype must accept at least the same range of types as its supertype declares.

In other words, the range of the argument types can expand, as shown here:

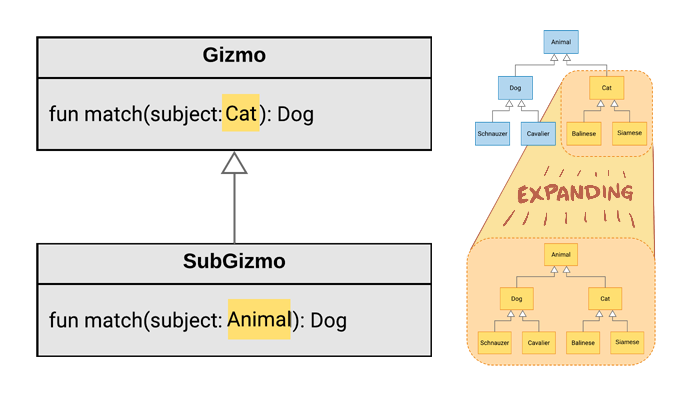
The range of types accepted in the match() function expanded from 3 types in Gizmo to 7 types in SubGizmo.

In the diagram above, the relationship between the containing type (Gizmo/SubGizmo) and its argument type (Cat/Animal) is called contravariance: as the Gizmo becomes more specific (that is, as it becomes more of a subtype), the type of the argument can become more general (that is, more of a supertype). They go in opposite directions.

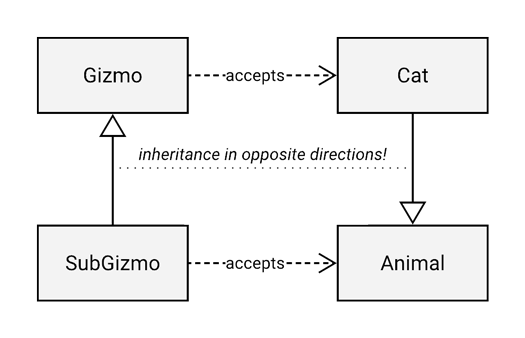
Even though this is safe for programming languages to do, Kotlin has followed Java’s lead, and does not allow for contravariance on argument types in normal class and interface inheritance, in order to allow for method overloading. There’s also a nifty workaround to this problem in Kotlin, if you’re interested.

But don’t worry - contravariance in argument types will make a comeback when we explore how these rules play out for generics in the next article.

Returning Results - Covariance

Here’s Rule #2:

A subtype must return at most the same range of types as its supertype declares.

This means it’s legal for a subtype to return a result that’s a “sub-er” type than the supertype declared. In other words, the range of the return types can narrow:

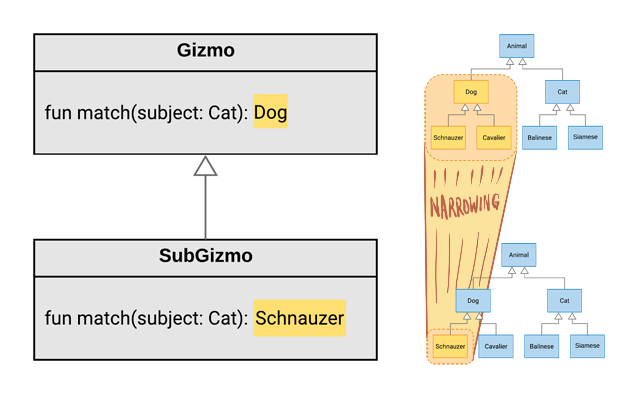
In this diagram, the match() function of Gizmo returns a Dog, but the subtype SubGizmo returns the subtype Schnauzer – the range of types returned narrowed from 3 types to 1 type. As our containing type becomes more specific, so can the return type! They can hold hands, becoming subtypes together. That’s why this relationship is called covariance. That’s co-, as in “together”.

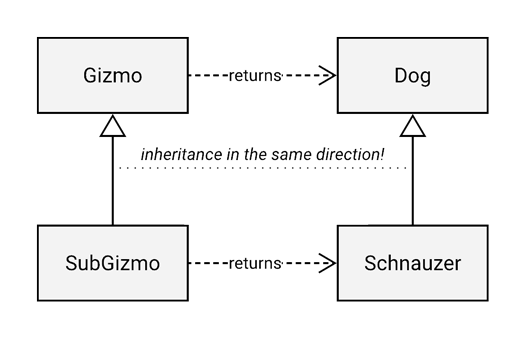
Kotlin does allow for covariant return types in normal class and interface inheritance:

interface Gizmo {
    fun match(subject: Cat): Dog
}

interface SubGizmo : Gizmo {
    override fun match(subject: Cat): Schnauzer
}

Invoking match() on a Gizmo reference will return a reference to a Dog (whose actual type is Schnauzer), whereas if match() is invoked on a SubGizmo reference, it’ll be returned as a Schnauzer.

val subGizmo = createSubGizmo()
val superGizmo = subGizmo as Gizmo

val dog = superGizmo.match(Cat())     // Inferred type is Dog
val schnauzer = subGizmo.match(Cat()) // Inferred type is Schnauzer

Summary

Wow, we’ve covered a lot of ground! We’ve seen how subtypes can safely expand the range of argument types and narrow the range of return types in functions. We’ve also seen how, for functions in regular class and interface inheritance, Kotlin supports covariance but not contravariance.

Things get even more fun when we see how these concepts play out for generics, and that’s the topic of the next article, The Ins and Outs of Generic Variance in Kotlin! See you there!