The Ins and Outs of Generic Variance in Kotlin

Have you ever wondered why generic variance works like it does? Or why Kotlin won’t let you use a type parameter as an argument when it’s marked as out? Have you wondered why the compiler sometimes won’t let you call a certain function on a generic?

Yes, generics can seem mysterious, but with just two simple, easy-to-understand rules, we can reason our way through almost everything related to variance.

In the last article, we discovered those two rules, and saw how they affect variance in normal class and interface inheritance. In this article, we’re going to use those same two rules to understand the why behind generic variance and type projections.

All right - here we go!

Generics and Subtypes

In the previous article, An Illustrated Guide to Covariance and Contravariance in Kotlin, we concluded these two rules about subtypes:

1. A subtype must accept at least the same range of types as its supertype declares.
2. A subtype must return at most the same range of types as its supertype declares.

If you haven’t already read that article, you should go check it out, because it demonstrates why these rules exist - in a visual way that makes them easy to remember.

To help work our way through the concepts in this article, we’re going to create our own generic collection, called Group. Let’s keep it simple by making it an interface instead of a class.

interface Group<T> {
	fun insert(item: T): Unit
	fun fetch(): T
}

Group is a simple collection that has two functions for interacting with the items that it contains - insert() for putting a new item into the group, and fetch() to get an item out of it.

What exactly are we going to be putting into our Group objects?

Animals!

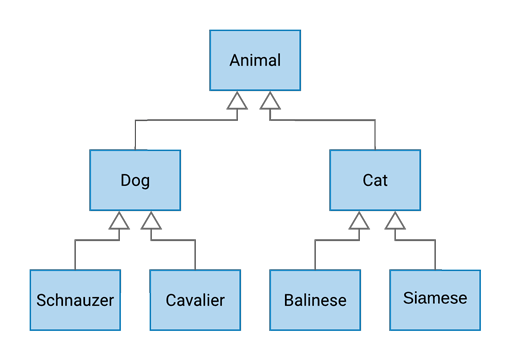
Yes, we’ll be using our Animal types from last time. Here’s what they look like:

We’re going to use the rules again. But instead of using them to demonstrate what you can do with inheritance, this time we’re going to start with a desired subtyping relationship (for example, “we want A to be a subtype of B”), and follow these two rules in order to make that relationship happen!

Let’s Make Us Some Covariance!

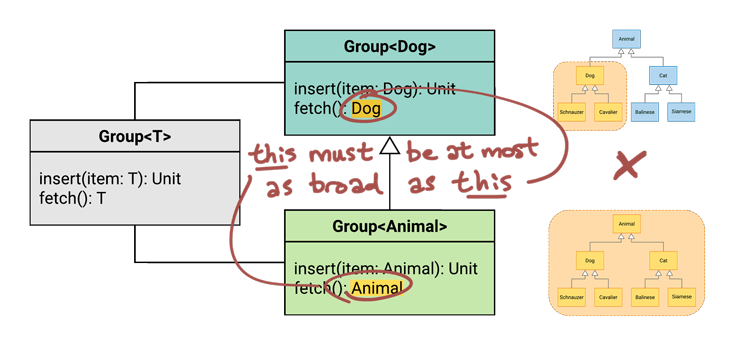
Let’s say our code is running a veterinarian’s office, and the doctors will be seeing a group of animals in the clinic today. If someone brings in a group of dogs, naturally, that should still count as a “group of animals”.

So we’ve got our desired subtyping relationship - we want Group<Dog> to be a subtype of Group<Animal>. (We call this a covariant relationship).

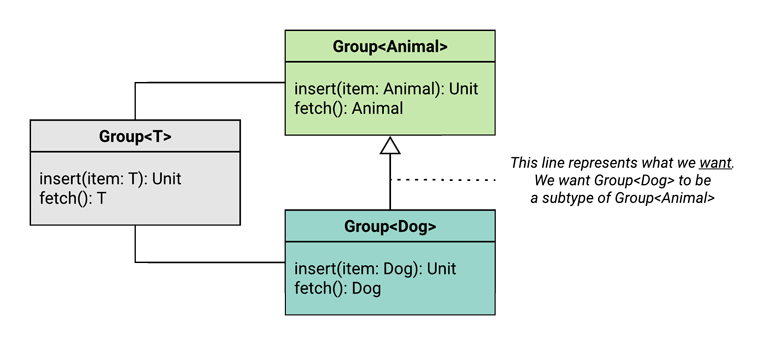
Now we just have to ask ourselves, “what must be true in order for Group<Dog> to be a subtype of Group<Animal>?”

We already have our two subtype rules.

1. A subtype must accept at least the same range of types as its supertype declares.
2. A subtype must return at most the same range of types as its supertype declares.

Instead of “subtype” and “supertype”, we’ll simply plug in the concrete types for the relationship that we want:

1. A subtype Group<Dog> must accept at least the same set of types as its supertype Group<Animal> declares.
2. A subtype Group<Dog> must return at most the same set of types as its supertype Group<Animal> declares.

Remember - both of those rules must be true in order for Group<Dog> to be a subtype of Group<Animal>.

Are they both true? Let’s find out!

Rule #1: Parameter Types

Does Group<Dog> accept at least the same set of types as Group<Animal>?

There’s only one parameter anywhere in our interface – it’s called item, and it’s on the insert() function. So now we just have to compare the type of that parameter in each of the Group types:

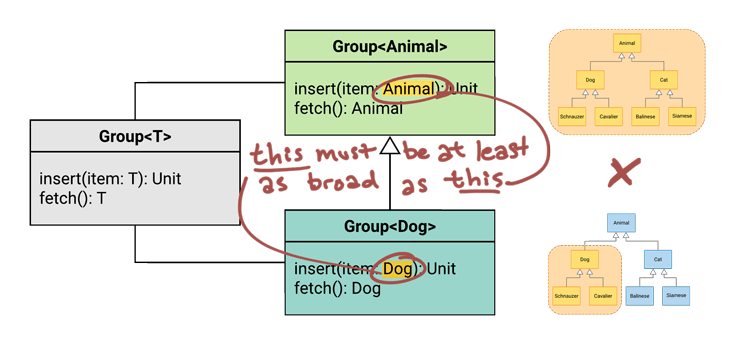
We see here that Group<Dog> does NOT accept at least the same range of types as Group<Animal>, because Dog is narrower than Animal.

Blast! We’ve already violated one of our two rules! Well, hold that thought - we’ll come back to it in a moment. Meanwhile, let’s check the second rule.

Rule #2: Return Type

Does Group<Dog> return at most the same set of types as Group<Animal>?

There’s only one result returned anywhere in our interface, and it’s on the fetch() function. Again, let’s compare the type of that result among our two Group types:

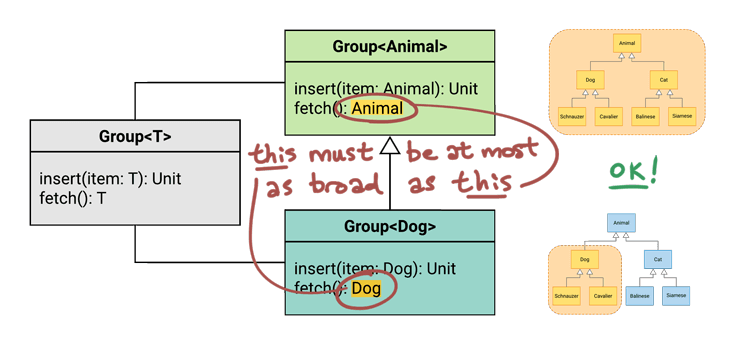
The fetch() function returns Dog, which is within the range of Animal. So, yes! We pass the second rule.

Dealing with Violations

So, we violated the first rule, but passed the second. Remember - in order to truly be a subtype, it must pass both rules. If either one of these rules is violated, we have to find some way to deal with that violation.

How can we do that?

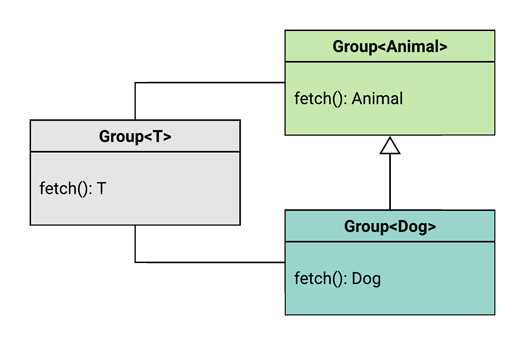
The obvious (but harsh!) answer is to simply remove the offending function entirely:

interface Group<T> {
	fetch(): T
}

By removing the insert() function, Rule #1 doesn’t even apply any more, because there are no longer any function parameters to consider!

Success! All that’s left is for us to tell the Kotlin compiler what we want. To do this, we put the out variance annotation on the type parameter T, like this:

interface Group<out T> {
	fetch(): T
}

It’s called out because T now only ever appears in the “out” position - as a function’s result type.

By doing this, Kotlin now knows to treat Group<Dog> as a subtype of Group<Animal>.

In fact, it will also enforce both of the subtype rules. So if you were to add the insert() method back, the compiler will show it as an error.

Type parameter T is declared as 'out' but occurs in 'in' position in type T

And now we know why Kotlin won’t let us put a type parameter in a function parameter position when it’s marked as out - it’s not type-safe because it violates Rule #1!

Creating Contravariance

Let’s change the scenario. Instead of a vet office, we’re now going to start a service where we’re going to take a dog, and find a group of good friends for it. If there’s a home with a group of dogs, that would work. But if there’s a whole farm of fun-loving animals, that would also work!

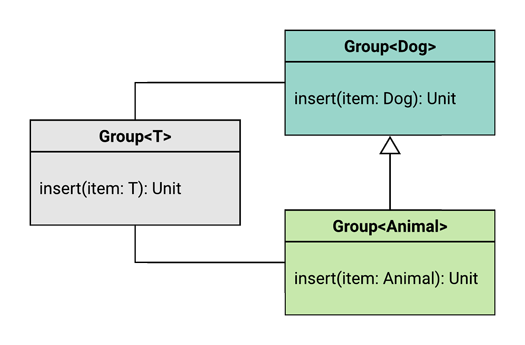
So in other words, this time, we want a Group<Animal> to be a subtype of Group<Dog>. This is called a contravariant relationship.

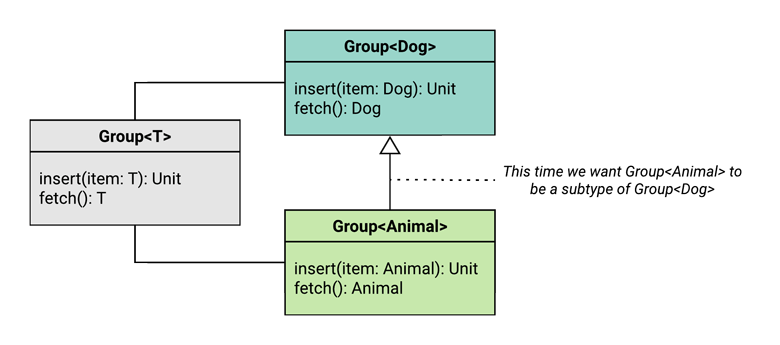
Again, we’re going to take our candidate subtype and supertype, and plug them into our two subtyping rules. (Note that Group<Animal> and Group<Dog> have swapped positions compared to where they were above, because we’re reversing the relationship!)

1. A subtype Group<Animal> must accept at least the same set of types as its supertype Group<Dog> declares.
2. A subtype Group<Animal> must return at most the same set of types as its supertype Group<Dog> declares.

Rule #1: Parameter Types

Does Group<Animal> accept at least the same set of types as Group<Dog>?

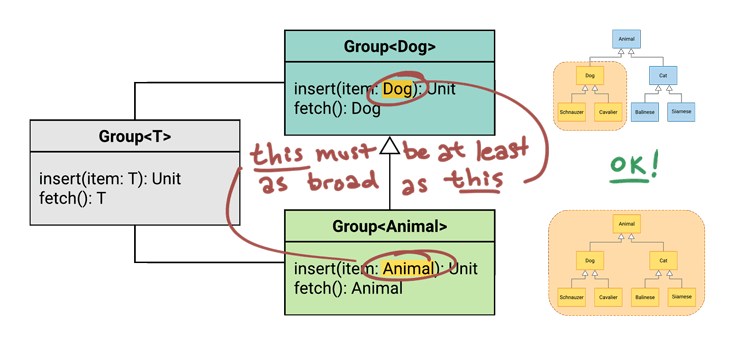
As we can see, the answer is yes. The only function parameter is item, and Animal encompasses everything that Dog does. So, rule #1 passes just fine.

Rule #2: Return Type

How about Rule #2?

Does Group<Animal> return at most the same set of types as Group<Dog>?

Rule #2 does not pass. The fetch() function of Group<Animal> returns Animal, which is a wider range than what Group<Dog>’s fetch() function returns.

Dealing with Violations

Again, we can deal with this violation by simply removing that function:

interface Group<T> {
	insert(item: T): Unit
}

Now, Rule #2 is no longer applicable, because T never shows up as a function’s result.

So, as before, all that we have left is to tell Kotlin that we want Group<Animal> to be a subtype of Group<Dog>, and we do that by adding the in variance annotation to T:

interface Group<in T> {
	insert(item: T): Unit
}

Voilà! Now the compiler will ensure that we don’t violate either of the two rules, so adding fetch() back into the interface would cause a compiler error.

Type parameter T is declared as 'in' but occurs in 'out' position in type T

And now it’s clear why Kotlin won’t let us use a type parameter as a result when it’s marked as in - it’s not type-safe because it violates Rule #2!

So there we go! We have managed to get the subtyping we wanted in both cases.

But hang on!

We had to pay a hefty price for it - in each case, we had to remove one of the two functions, because in each case, one of the two subtyping rules was violated.

What if we need to keep both of those functions?

Keeping Both of Those Functions

One option is to split the interface into multiple interfaces - one with the insert() function, and one with the fetch() function.

interface WritableGroup<in T> {
	fun insert(item: T): Unit
}

interface ReadableGroup<out T> {
	fun fetch(): T
}

You’d probably still want a Group interface that includes both of those functions, and that’s easy enough to create:

interface Group<T> : ReadableGroup<T>, WritableGroup<T>

Now, anywhere in our code that we want to call fetch(), we use ReadableGroup, and anywhere that we want to call insert(), we use WritableGroup:

fun read(group: ReadableGroup<Dog>) = println(group.fetch())
fun write(group: WritableGroup<Dog>) = group.insert(Dog())

Splitting up interfaces does the trick, but it’s certainly more code to write. Wouldn’t it be nifty if Kotlin gave us some way to effectively split the interfaces for us, without having to write those interfaces ourselves?

In fact, it does! Here’s how that looks:

fun read(group: Group<out Dog>) = println(group.fetch())
fun write(group: Group<in Dog>) = group.insert(Dog())

Until now, we’ve put the variance annotations (out and in) on the type parameter - at the point in the code where we declared the generic, which is why we call it declaration-site variance.

But here, we put the variance annotations on the type argument instead - at the point in the code where we’re using the generic, so we call it use-site variance.

The result?

Type Projections

The group parameter in both of these functions is now a type projection.

• Group<out Dog> is almost effectively the same as our ReadableGroup<Dog> interface, and…
• Group<in Dog> is almost effectively the same as our WritableGroup<Dog> interface.

Why almost?

Because here’s what their effective interfaces actually look like compared to the readable/writable interfaces we created above:

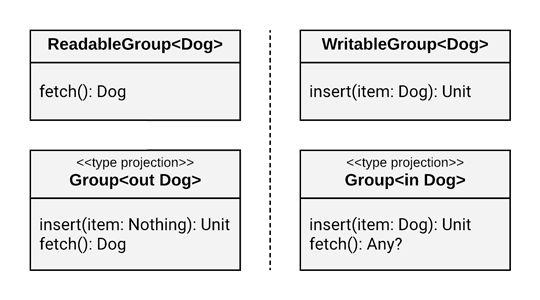
By using a type projection instead of our own, split interfaces, we still have both functions present in each case.

But did you notice the types?

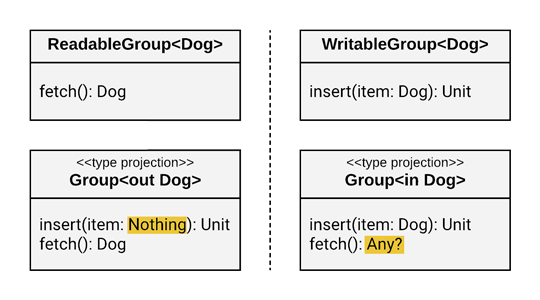
Why did Kotlin use those types? Let’s find out…

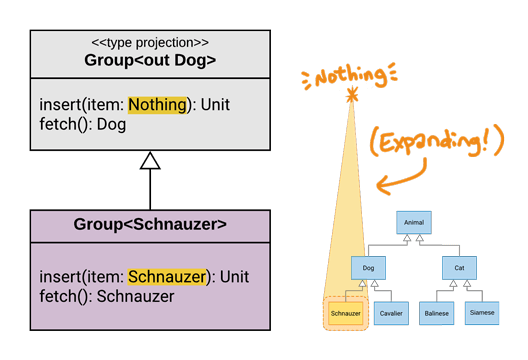
Out-Projection

In the case of the out-projection, the type of the item parameter type was changed from Dog to Nothing, which is the magical subtype of every type in Kotlin.

This doesn’t sound very helpful - you won’t actually be able to call insert(), because you can never have an instance of Nothing.

But when we line it up against Rule #1, it makes perfect sense! For example, in order for a Group<Schnauzer> to be a subtype of Group<out Dog>, it must accept at least the same range of types as Group<out Dog> accepts. And since every single type is broader than Nothing, it satisfies the rule!

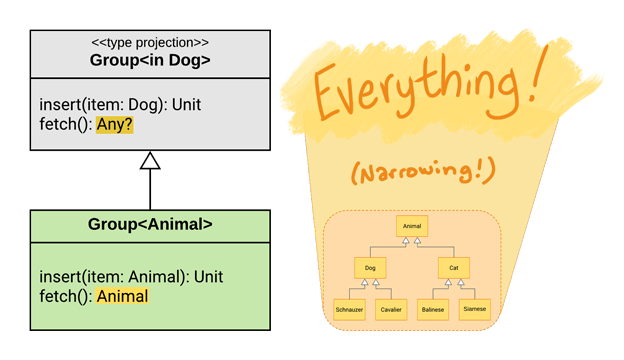
In-Projection

In the case of the in-projection, the return type of fetch() was changed from Dog to Any?. So, with WritableGroup<Dog>, we weren’t able to call fetch() at all. But with Group<in Dog>, you can call it – you’re just going to get it back as an Any?. For some use cases, this might still be helpful, like if you just want to send it along to println().

As you probably guessed, this works to satisfy Rule #2. A Group<Animal> must return at most the same range of types as Group<out Dog>. Since Any? is the-same-or-broader-than every type, the rule is satisfied.

And now it makes sense why Kotlin changes function signatures on type projections - it’s simply upholding the two subtyping rules!

Summary

Between the last article and this one, we’ve covered a lot! We’ve seen why in and out affect generics like they do - in both declaration-site variance and type projections, achieving both covariance and contravariance along the way.

But what if we want to accept every possible kind of a particular generic - such as every possible Group?

In the next article, Star-Projections and How They Work, we’re going to apply these two subtyping rules (one more time!) in order to fully understand - at a foundational level - the three different ways that you can accomplish this. See you then!

For more information, you can also check out the official documentation about generics in Kotlin.