Star-Projections and How They Work

Have you ever wondered how star-projections work? Or why they change your function parameter and return types? Or why it seems like sometimes you can actually get by without them?

In the first article in this series, An Illustrated Guide to Covariance and Contravariance in Kotlin, we uncovered two simple, easy-to-understand rules that illuminate variance, and saw how they applied to regular class and interface inheritance in Kotlin.

In the second article, The Ins and Outs of Generic Variance in Kotlin, we saw how those same two rules played out for generics, discovering what type projections are and how they work.

In this third and final article in the series, we’re going to apply these same two subtyping rules to a special case - accepting all kinds of a generic.

Wanna know what’s cool? Star-projections are actually only one way to handle this case! In this article, we’ll explore all three ways that you can solve this problem. Along the way, we’ll gain an understanding of exactly why star-projections work the way that they do.

Ready? Let’s rock and roll!

Accepting All Kinds of a Generic

There are times when you want a function that can accept any kind of a particular generic. For example, let’s say we’ve got this Group interface, which we also used in the last article:

interface Group<T> {
  fun insert(item: T): Unit
  fun fetch(): T
}

We’re interested in creating a function that can accept absolutely any kind of Group at all. We want it to accept:

• Group<Dog>
• Group<Animal>
• Group<Int>
• Group<String>
• Group<Group<Number>>
• Group<Whatever>

In other words, we want to create some kind of “super group” type that is the supertype of every possible kind of Group imaginable.

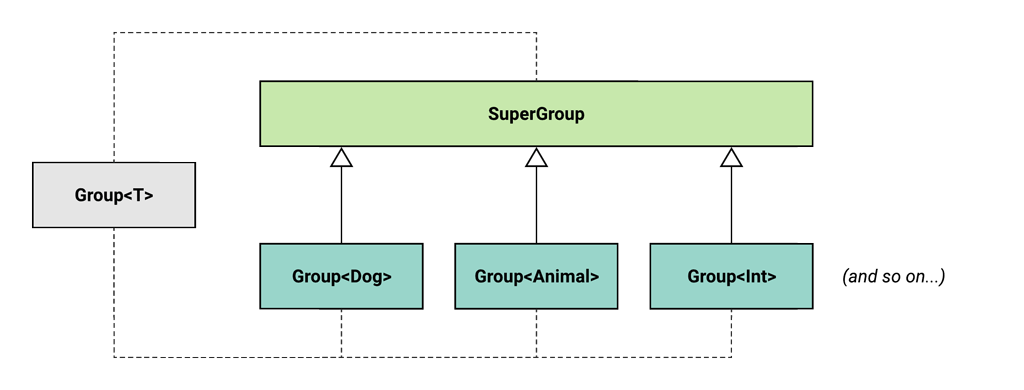
How can we achieve this in a type-safe way?

Well, let’s use our two subtyping rules to guide us to some solutions. As you recall, these are the two rules:

1. A subtype must accept at least the same range of types as its supertype declares.
2. A subtype must return at most the same range of types as its supertype declares.

Remember - in order for a subtyping relationship to truly exist - in order for a subtype to truly be a subtype, and in order for a supertype to truly be a supertype - the relationship must adhere to both of these rules!

Just like in the last article, we’re going to take the relationship that we want, and plug it into those rules. So in our case, we want every kind of group to be a subtype of our super group (which we’ll name SuperGroup), so let’s rewrite the rules to represent that!

1. A subtype Every kind of Group must accept at least the same set of types as its supertype SuperGroup declares.
2. A subtype Every kind of Group must return at most the same set of types as its supertype SuperGroup declares.

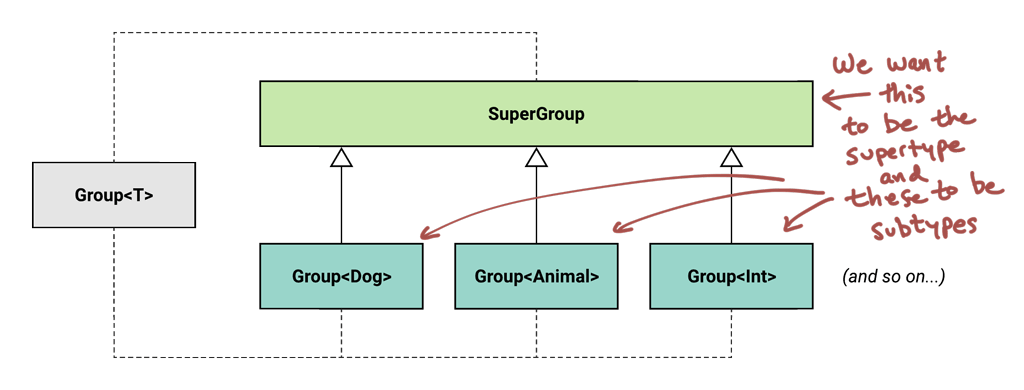
Now that those rules are tailored to our situation, we just have to find a way to satisfy them both. How can we do that?

Satisfying Rule #1

Every kind of Group must accept at least the same set of types as SuperGroup declares.

In order for every kind of Group to accept at least the range of types that SuperGroup declares, SuperGroup has to declare the smallest range possible. Every type must be a supertype of it.

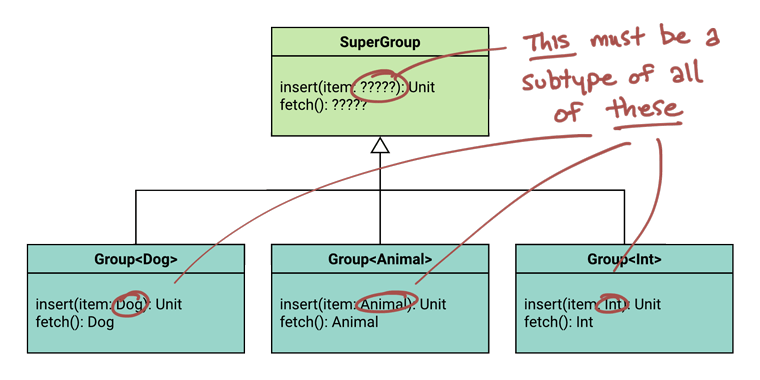
Any guesses what type that is in Kotlin?

It’s the Nothing type! Nothing is a magical type that:

1. is the subtype of every type, and
2. can never be instantiated

So, in our SuperGroup, everywhere that the type parameter was used as an argument, we’ll need to use Nothing instead.

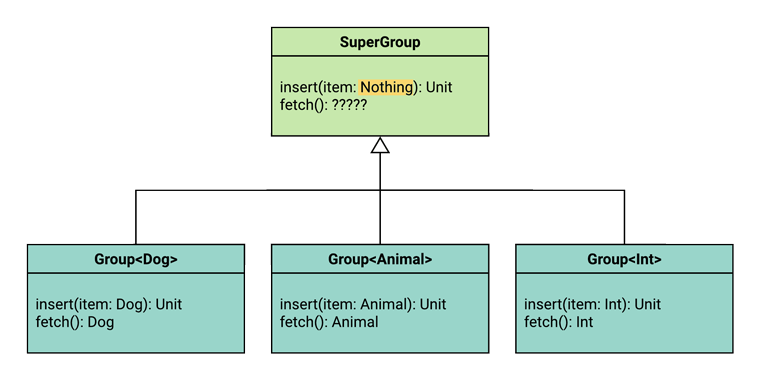
That takes care of Rule #1! We’re halfway there!

Satisfying Rule #2

Every kind of Group must return at most the same set of types as SuperGroup declares.

Now, according to Rule #2, we also need every kind of Group to return at most the same range of types as SuperGroup declares. In order for that to be true, SuperGroup must declare the largest range possible - every type must be a subtype of it.

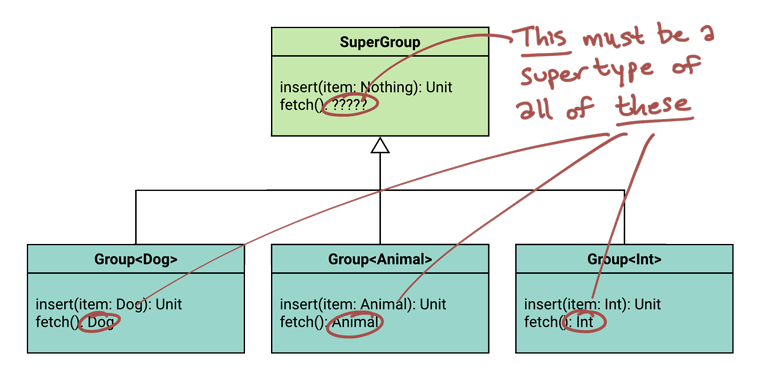
What’s at the top of the type hierarchy in Kotlin? What’s the supertype of every type? As you know, it’s Any?.

So, in order to satisfy Rule #2, the SuperGroup will need to return Any? on all functions that specify the type parameter as the result.

Easy!

Creating the SuperGroup

Well, look at that!

Using nothing more than the same two subtyping rules we’ve been using all along, we’ve reasoned our way to a generic type that can accept any kind of Group!

We’ve concluded that, for every function that accepts or returns the type parameter, our SuperGroup will need to:

1. Accept Nothing
2. Return Any?

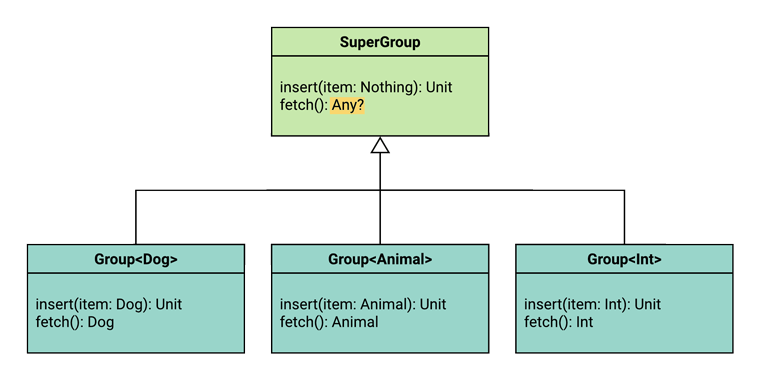
In other words, the interface needs to look like this:

interface SuperGroup {
    fun insert(item: Nothing): Unit
    fun fetch(): Any? 
}

It might be tempting to just create this interface in your code and have Group extend it, but that actually won’t work!

Why not?

Because, as you might recall, Kotlin does not support contravariant argument types in normal class and interface inheritance. But good news - we can achieve the same thing with a type projection!

Type Projections that Accept All Kinds of a Generic

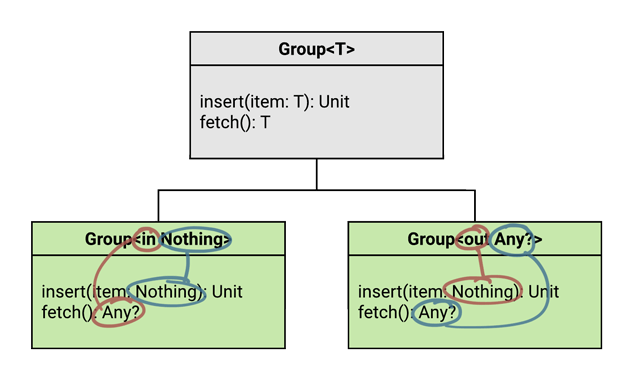
How can we create a type projection that, for its type parameter, accepts Nothing and returns Any??

Interestingly, there are two perspectives that you can take on this. You could either:

1. Use an in-projection, and specify Nothing as the type argument.
2. Use an out-projection, and specify Any? as the type argument.

In either case, we achieve the same thing - just from different angles! Here are the effective definitions in each case:

See those function signatures? Same-same.

In case you’re wondering why that’s so, remember that:

• In-projections set the return types to Any?
• Out-projections set the argument types to Nothing

If you put those together with the type arguments in each case, you get the same function signatures.

But guess what - there’s also a third option!

Star-Projections

Instead of using Group<in Nothing> or Group<out Any?>, you can just use Group<*>. It produces the same effective interface as the other two approaches:

As you probably guessed, we call this a star-projection because for the type argument, we specify an asterisk, which looks like a star.

So then, we have three ways that we can accept any kind of a generic:

• in-projection - <in Nothing>
• out-projection - <out Any?>
• star-projection - <*>

While any one of these three approaches technically can be used, star-projection is the idiomatic way to solve this problem in Kotlin, and should be favored over the other approaches.

Why is this?

Well, when you look at a star-projection, you don’t have to think about it much. Anyone who’s spent time on an operating system command line is accustomed to thinking of * as a wildcard that’s used to match anything - like ls *.txt. It’s a similar idea here - we associate the * with the notion of accepting a Group that has any kind of type argument.

But beyond that, there are some fascinating differences once you introduce a type parameter constraint!

Let’s take a look!

Projections and Type Parameter Constraints

A type parameter constraint limits the instances of a generic so that the type parameter has an “upper bound”. For example, let’s update our Group interface with a constraint:

interface Group<T : Animal> {
  fun insert(member: T): Unit
  fun fetch(): T
}

By adding : Animal to the type parameter, you can now only create a Group of type Animal, or subtype of Animal. So, for instance, Group<Animal> and Group<Dog> are fine, but Group<String> and Group<Int> are no longer valid - the compiler will reject them with this quite sensible error message:

Type argument is not within its bounds

Let’s see how each of our three approaches fare when dealing with constraints…

In-Projections and Constraints

Here’s a function that reads from the Group, using in-projection:

fun readIn(group: Group<in Nothing>) {
  // Inferred type of `item` is `Any?`
  val item = group.fetch()
}

Kotlin does some type inference here, and it identifies the type of item as Any?.

Yes, you and I know that the type parameter constraint we added means that item can never be a String or Int, or anything more general than an Animal. So it seems like Kotlin could safely assume that the result of fetch() is at most an Animal.

But the in-projection doesn’t take this into account. It still uses Any? as the result type from fetch(). Bummer.

Out-Projections and Constraints

Now here’s a function that reads from a Group using out-projection. So far, we’ve said that the way to accept all types using an out-projection is to use <out Any?>, but once you introduce a type parameter constraint, Any? will no longer work! The most general type we can use is the upper bound of our type parameter constraint.

So in our case, we can now satisfy Rule #2 by using <out Animal> instead of <out Any?>. And in fact, the Kotlin compiler no longer even allows us to specify Any? as the type argument! We have to set it to Animal at most:

fun readOut(group: Group<out Animal>) {
  // Inferred type of `item` is `Animal`
  val item = group.fetch()
}

Here, we see that the result of fetch() is considered an Animal instead of Any?. This is fantastic, because it means we can do more with item in readOut() than we could do in readIn() - we can invoke all of Animal’s functions and properties on item.

Star-Projections and Constraints

And finally, here’s a similar function that reads from a Group using star-projection.

fun readStar(group: Group<*>) {
  // Inferred type of `item` is `Animal`
  val item = group.fetch()
}

Just like with readOut() above, Kotlin will take type parameter constraints into account - the returned type from fetch() in this case is Animal. Again, this is great because we can treat item like an Animal, invoking functions or accessing properties.

Changing the Constraint

Now for the fascinating part!

What would be the impact to our three different functions - readIn(), readOut(), and readStar() - if we were to change the constraint from Animal to Dog?

interface Group<T : Dog> {
  fun insert(member: T): Unit
  fun fetch(): T
}

Here’s what would happen:

readIn() would be unaffected, still inferring Any? as the type of item

fun readIn(group: Group<in Nothing>) {
  // No change - inferred type of `item` is `Any?`
  val item = group.fetch()
}

readOut() would get a compiler error on the type argument - you’d have to change Group<out Animal> to Group<out Dog>. When you make that change, then the inferred type of item would change to Dog.

// Gotta change the type argument here to `Dog`!
fun readOut(group: Group<out Dog>) {
  // Inferred type of `item` is now `Dog`
  val item = group.fetch()
}

And our star-projection? Well, readStar() would still compile, and would automatically update the inferred type of item to Dog. Brilliant!

// No change to the function signature!
fun readStar(group: Group<*>) {
  // Inferred type of `item` is `Dog`
  val item = group.fetch()
}

So, there are some practical benefits to using star-projections - not only are they easier to read and understand, but they also more gracefully handle changes to type parameter constraints!

How <*> Differs from <Any?>

Finally, let’s clear up a common point of confusion.

Why is it that you can use <Any?> in some cases, but you have to use <*> in other cases? For example, here are two functions - one accepting a List<Any?> and the other accepting a List<*>.

(Note that we’re using List<Any?> here, not List<out Any?>).

fun acceptAnyList(list: List<Any?>) {}
fun acceptStarList(list: List<*>) {}

Now let’s send a List<String> to each of them:

val listOfStrings: List<String> = listOf("Hello", "Kotlin", "World")

acceptAnyList(listOfStrings)
acceptStarList(listOfStrings)

If you try this out, you’ll see that it works just fine! Both functions end up accepting a List<String>. But if you were to change this to an Array, you’ll quickly notice that it won’t compile:

fun acceptAnyArray(array: Array<Any?>) {}
fun acceptStarArray(array: Array<*>) {}

val arrayOfStrings = arrayOf("Hello", "Kotlin", "World")
acceptAnyArray(arrayOfStrings)  // Compiler error here
acceptStarArray(arrayOfStrings)

The call to acceptAnyArray() fails with this compiler error:

Required: Array<Any?> Found: Array<String>

What’s going on here?

As you might recall, generics are invariant by default. In other words, compilation fails here because Array<Any?> is not a super type of Array<String>. The array you pass to this function would have to be exactly of type Array<Any?> - Array<String> doesn’t count.

So why did this work with List but not with Array?

Because in the Kotlin standard library, List (unlike Array) is using declaration-site variance to specify its type parameter as out. So when you specify a function parameter of List<Any?>, you’re effectively getting List<out Any?>, which, as we saw above, is one of the three ways to accept all kinds of a generic.

Summary

We’ve discovered three ways to accept all kinds of a generic:

• Using out-projection: <out Any?>
• Using in-projection: <in Nothing>
• Using star-projection: <*>

Star-projection is the favored approach, because it’s idiomatic Kotlin. It’s easy to read and understand, and it handles type parameter constraints gracefully. And now you know how and why they work!

This concludes the series on generic variance. I hope it’s helped you establish a solid foundation from which to understand everything about variance in Kotlin (and other programming languages, too!).

I’m looking forward to exploring some other fascinating aspects of Kotlin in upcoming articles!